基于单次散射的天空大气渲染方法

最近KongEngine实现了IBL(Image Based Lighting)，可以将HDR环境贴图映射作为3D场景的环境。

在实现了IBL之后我又产生了一个想法，能否实现类似UE中的大气环境的渲染效果呢？我尝试去寻找答案，发现如果要完全复刻UE中的效果确实需要一定的功夫的，但是最基础的天空大气渲染并没有想象中那么复杂，于是我便花了点时间在KongEngine中实现了这个功能。

我打算将这个方法的基础思想和实现在此简单记录一下。

单次散射模型

星球的大气层是一种参与性介质，和在真空环境不同，光在大气层中传播的时候会因为大气中的微小颗粒（水、灰尘等等）发生散射（折射、反射）和吸收等情况。因此我们看向空中的一个点的时候，这个点的颜色是光经过多次散射得到的结果。

光到达我们眼睛之前经过多少次反射和折射是不一定的，在实时渲染的需求下计算太多次光的变化显然也是不显示的。最简单的方法，是使用单次散射模型：我们假定光在进入我们眼睛之前，有且只发生了一次散射。光一般在第一次散射的时候，还会有最多的能量剩余，后面的多次散射能力相对少，对最后效果的呈现也影响不大，因此这种模型可以在保证性能的情况下，还有不错的效果。

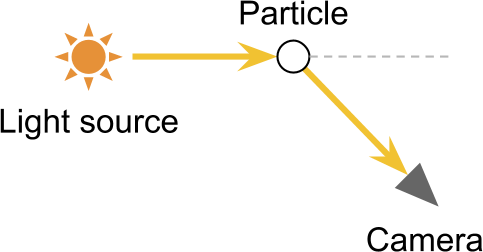
除了散射，光在传播的时候会被大气吸收。一般来说，如果在一个均匀的介质中传播的话，光的被吸收的部分和介质的密度，以及传播的路径长度正相关。放到单散射模型的例子中，就是需要计算光在散射前和散射后的路径上，被吸收了多少能量。

按照上面的图，假设相机在A点，观察方向为AB，其中有一束光在P点发生散射后沿着PA进入相机。如果我们知道了光线损耗和距离相关的公式，那么似乎是只要计算出CP和PA的长度，在带入公式后就可以得到光该路径上传播后的最终能量了。

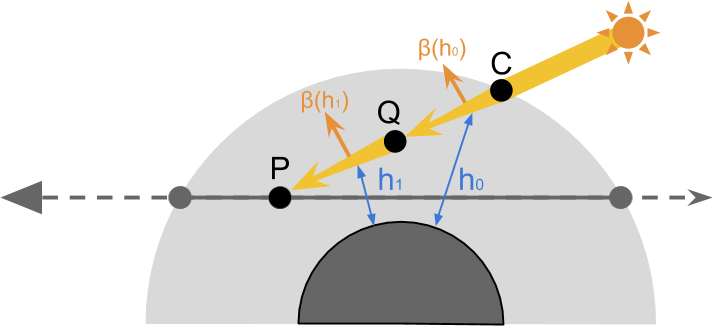
但是对于大气层来说，它的密度并不是均匀的，而是和大气层距离地面的高度相关。所以在计算CP段光线损耗的时候，我们需要将这段距离分为多个小段，每个小段的损耗公式带入对应平均高度，在最后将所有结果相加才。小段划分的越密集，则结果越准确。

如果我们还要考虑大气中的其他因素，比如说大气中的云层，在这些区域中光的损耗就不仅仅是和高度相关了。

另外一点就是，当我们考虑AB方向的光线时，它的最终效果，是在大气层内的所有AB连线上面的点的散射结果的总和（P0、P1、P2…Pn），因此我们也同样的需要对AB线段进行分段采样并将结果叠加。AB线段上的每一个采样结果按照上面所描述的计算单一P点的方式。

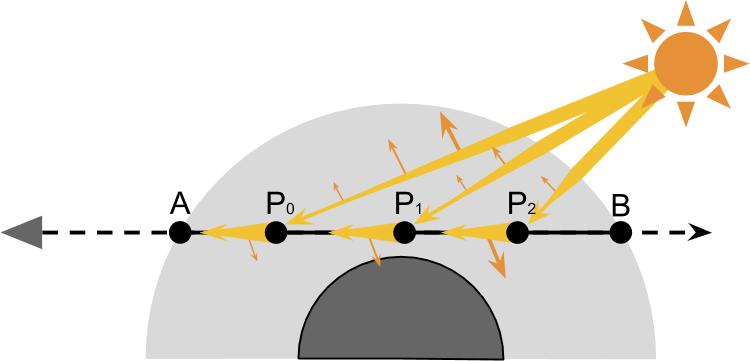
以上便是大气单次散射模型的基本思路。

散射的计算

之前我们提到了计算光的散射，这里我们介绍一下散射的相关计算。会提及一些公式，但是不会做过多的数学推导工作，对推导过程感兴趣的可以看一下文章中的参考资料。

一般来说，天空大气的散射主要包括两种，分别是瑞利散射和米氏散射。

• 瑞利散射是当光线通过介质中的微小颗粒或分子时发生的散射现象。由于颗粒或分子的尺寸远小于光的波长，不同波长的光线会以不同的角度散射，一个最经典的案例就是因为蓝色的波长是较短的，所以蓝色很容易发生瑞利散射，导致天空呈现蓝色。
• 米氏散射则一般由空气中含有的较大颗粒的介质，如气溶胶、灰尘、水滴等引起。和瑞利散射不同的是，米氏散射和光的波长关系并不大。
  

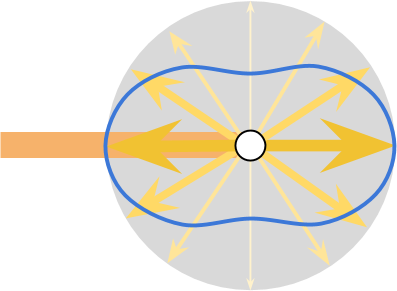
那么根据前面的模型思路，光在P点上发生了散射，其中一部分能量沿着PA方向进入相机的实现。获取这一部分能量的计算函数被称之为相位函数（Phase Function）。相位函数是用来描述，当光线发生散射的情况时，某个方向（一般是和原光线方向的夹角）占原光线的能量的比例。瑞利散射和米氏散射的相位函数是不同的，同一种散射的相位函数也会有不同的方法进行拟合，这里我不想去做过多的公式推导的工作，有兴趣的可以去查看参考资料的推导过程。

下方是瑞利散射的相位函数，theta是原光线方向和目标方向的夹角：

$$\begin{array}{rl}P(\theta )& =\frac{3}{16\pi }(1+co{s}^2\theta )\end{array}$$

下方是米氏散射的相位函数，这里使用的是Henyey-Greenstein函数来近似。

$$P(\theta )=\frac{1-g^2}{4\pi (1+g^2-2gcos(\theta ){)}^{3/2}}$$

好了，现在我们知道了如何计算光线在P点的散射行为。剩下的工作就是需要计算光线在传播过程的损耗了。这一部分的计算方法称之为衰减系数，或者消光系数。消光系数中的一部分，需要对光线在传播的路线的长度和空气密度进行积分。在程序中的表示就是将光的传播路径分为小段，将每一小段的长度和平均密度（或者小段中点的介质密度）相乘而得到，这个结果我们称之为光学距离（Optical Depth）。

衰减系数的计算公式如下，红色部分代表的是在海拔为h的散射系数。他可以分解为在海平面上的散射系数乘以在海拔h的介质密度。

$$T(PA)=\exp -{\int }_P^A\beta (\lambda ,h)ds$$

分解出来后得到的结果如下，其中红色的部分代表的意思是在海平面的散射系数，是一个常量，黄色部分代表了在海拔为h的介质的密度。这个公式的积分便是针对AP路线上的介质密度，其结果也就是光学距离。

$$T(PA)=\exp -\beta (\lambda ){\int }_P^A\rho (h)ds$$

介质密度的计算公式如下，其中H代表的是一个基准海拔，是一个常量。不同散射的基准海拔有所不同，瑞利散射的基准海拔是*8500*，而米氏散射的基准海拔是*1200*。

$$\rho (h)=\exp (-\frac{h}{H})$$

自此，我们关于单次散射的天空大气渲染方法的基本预备知识已经了解的差不多了，接下来介绍shader的相关代码。

Shader代码

首先，为了计算AB、PC等视线和光线在大气层内的传播距离，我们需要一个函数来计算射线和球体的相交情况。

vec2 ray_sphere_intersection(vec3 ray_origin, vec3 ray_direction, vec3 sphere_center, float sphere_radius)
{
    // ray-sphere intersection that assumes
    float a = dot(ray_direction, ray_direction);
    vec3 oc = ray_origin - sphere_center;
    float b = 2.0 * dot(ray_direction, oc);
    float c = dot(oc, oc) - (sphere_radius * sphere_radius);
    float d = (b*b) - 4.0*a*c;

    // 返回击中结果，y小于x代表无结果
    if (d < 0.0) return vec2(1e10,-1e10);
    // 击中的话有两个相同或者不同的结果
    return vec2(
        (-b - sqrt(d))/(2.0*a),
        (-b + sqrt(d))/(2.0*a)
    );
}

好了，那有了这个辅助公式，我们正式开始计算大气的颜色。首先，按照之前的理论，我们要计算视线向量在大气层内的长度，所以我们对射线方向和大气层，以及射线方向和星球表面做射线检测。得到视线在大气层内的长度后，根据我们预设的想要采样的步数（iSteps），计算出每次采样的长度ds。

ray_dir = normalize(ray_dir);

// 视线和大气层大小的尺寸的射线检测
// x为大气入射点的距离、y为大气出射点的距离（x==y代表光线和大气球体相切，x>y代表光线不经过大气）
vec2 atmos_hit = ray_sphere_intersection(ray_origin, ray_dir, rAtmos);
// 未击中，返回0
if (atmos_hit.x > atmos_hit.y) return vec3(0,0,0);

    // 视线和星球做射线检测，取得近处的检测结果（远处的那个光被星球本体遮挡）
vec2 planet_hit = ray_sphere_intersection(ray_origin, ray_dir, planet_radius);
float light_distance = atmos_hit.y;

// hit the planet
if(planet_hit.x < planet_hit.y && planet_hit.x > 0.1)
{
    light_distance = planet_hit.x;
}

// light sample length
float ds = light_distance / float(iSteps);

那么接下来，便是进入采样的循环。循环有两层，外面的循环是计算视线方向上的每个采样点的光能量，而计算这个点的光能量也需要一个循环，这个循环是用于采样该点和光源之间的连线在大气层内的线段（也就是之前图片的PC段）的光学距离。根据前面提到的公式，光学距离乘以海平面的散射系数便可以得到光的衰减系数，因此jSteps循环可以得到光线在进入大气层后，传播到达视线上的采样点（P0、P1...Pn点）的衰减所剩下的能量。

// Initialize the primary ray time.
float iTime = 0.0;

// Initialize accumulators for Rayleigh and Mie scattering.
vec3 total_scatter_rlh = vec3(0,0,0);
vec3 total_scatter_mie = vec3(0,0,0);

// Initialize optical depth accumulators for the primary ray.
float total_od_rlh = 0.0;
float total_od_mie = 0.0;

// 对每个视线上的采样点循环
for (int i = 0; i < iSteps; i++) {
    // 获取到采样点的位置
    vec3 iPos = ray_origin + ray_dir * (iTime + ds * 0.5);

    // 在当前点向太阳的位置做射线检测，以大气的半径为球体。.y是代表大气的出射点，j_steps代表采样数
    float jStepSize = ray_sphere_intersection(iPos, pSun, rAtmos).y / float(jSteps);

    float jTime = 0.0;
    float jOdRlh = 0.0;
    float jOdMie = 0.0;

    // 在当前采样到大气入射点的距离上，采样计算
    for (int j = 0; j < jSteps; j++) {
        // 计算采样点到光源的衰减
        vec3 jPos = iPos + pSun * (jTime + jStepSize * 0.5);

        float jHeight = length(jPos-planet_center) - planet_radius;

        // Accumulate the optical depth.
        jOdRlh += get_atmos_density(jHeight, scale_height_rlh) * jStepSize;
        jOdMie += get_atmos_density(jHeight, scale_height_mie) * jStepSize;

        // Increment the secondary ray time.
        jTime += jStepSize;
    }

    // 观察点和星球表面距离
    float surface_height = length(iPos-planet_center) - planet_radius;

    // 计算这一步的散射的光学深度结果
    float od_step_rlh = get_atmos_density(surface_height, scale_height_rlh) * ds;
    float od_step_mie = get_atmos_density(surface_height, scale_height_mie) * ds;
    
    total_od_rlh += od_step_rlh;
    total_od_mie += od_step_mie;

    // 计算衰减系数，光在经过一定距离后衰减剩下来的比例。
    vec3 attn = exp(-(kMie * (total_od_mie + jOdMie) + kRlh * (total_od_rlh + jOdRlh)));

    // Accumulate scattering.
    total_scatter_rlh += od_step_rlh * attn;
    total_scatter_mie += od_step_mie * attn;

    // Increment the primary ray time.
    iTime += ds;
}

计算瑞利散射和米氏散射的大气密度的代码如下所示，其中scale_height在计算瑞利散射的时候带入的是8500，米氏散射则带入1200。

// 获取大气密度
// 传入位置离海平面的高度，以及散射的相关基准高度
// 大气中任意一点的散射系数的计算，简化拆解为散射在海平面的散射系数，乘以基于海平面高度的该散射的大气密度计算公式
float get_atmos_density(float height_to_sea_level, float scale_height)
{
    return exp(-height_to_sea_level / scale_height);
}

将iSteps循环的结果累加起来，我们便得到了视线上（AB）的每个采样点的光能量传播到达相机（A点）经过衰减的能量的和。那么还剩一个部分，就是光在P点进行散射的时候，光也损失掉了一部分能量，这个过程可以通过乘以米氏散射和瑞利散射的相位函数来计算。因为每个采样点P的结果都需要乘以相位函数，所以我们可以将它提取到最外面，乘以光的能量的总和即可。

不过需要注意的是，前面的公式提到了，相位函数是和光线入射方向和目标方向的夹角相关的，所以如果我们默认太阳光源是平行光的话，这个夹角对每个采样点来说是一样的，所以可以将相位函数提取到最外层。如果认为这个夹角对每个采样点不一样的话，那也许还是应该老老实实在计算每个采样点的光的时候单独去处理。

最终的结果除了乘以相位函数，还需要乘以海平面的散射系数，结果如下。

// 计算并返回最终颜色
// iSun是光源（太阳）的颜色
return iSun * (pRlh * kRlh * total_scatter_rlh + pMie * kMie * total_scatter_mie);

下面是得到的结果：

参考资料

• https://www.alanzucconi.com/2017/10/10/atmospheric-scattering-1/
• https://www.xianlongok.site/post/8e5d3b12/